The universe has always fascinated humanity, inspiring countless questions about the motion of celestial bodies. Among the many scientific breakthroughs in astronomy, Kepler’s Laws of Planetary Motion stand out as pivotal in shaping our understanding of planetary orbits. These laws, formulated by the German astronomer Johannes Kepler in the early 17th century, describe how planets move around the Sun. 

Who was Kepler?

Johannes Kepler (1571–1630) was a German mathematician, astronomer, and astrologer. He is best known for formulating the three laws of planetary motion describing how planets orbit the Sun. Kepler’s work marked a significant shift in our understanding of the cosmos and laid the groundwork for modern astronomy and physics.

Kepler initially worked as an assistant to Tycho Brahe, a renowned Danish astronomer known for accurately observing celestial bodies. Using Brahe’s meticulous data, Kepler analyzed the motion of planets, particularly Mars, and discovered that their orbits were not circular, as previously believed, but elliptical.

Kepler’s achievements were revolutionary for several reasons:

1. Elliptical Orbits: His discovery that planets move in elliptical orbits (Kepler’s First Law) contradicted the long-held belief in perfect circular orbits.
2. Planetary Speed Variation: He showed that planets move faster when closer to the Sun and slower when farther away (Kepler’s Second Law).
3. Orbital Relationship: His third law revealed the mathematical relationship between a planet’s orbital period and its distance from the Sun.

Significantly, Kepler was also a key figure in the Scientific Revolution and his ideas influenced other great scientists, including Isaac Newton, who later formulated the law of universal gravitation based on Kepler’s findings. Beyond his laws, Kepler contributed to optics and proposed theories about planetary motion that continue to inspire modern science. Let’s explore these laws in simple terms and understand their significance in modern astronomy.

Kepler’s First Law: The Law of Ellipses

Kepler’s First Law states that planets move in elliptical orbits with the Sun at one focus. An ellipse is an oval-shaped curve, different from a perfect circle. This was a groundbreaking discovery because it overturned the long-held belief that planets moved in circular orbits.

Imagine drawing an ellipse with two fixed points called focal points. The Sun occupies one of these focal points, while the other remains empty. The shape of the ellipse depends on how far apart the focal points are. If the focal points are close, the ellipse looks more like a circle. If they are farther apart, the ellipse becomes more stretched.

This law helps astronomers understand the true paths of planets and provides a foundation for calculating their positions at any given time. For example, Earth’s orbit is nearly circular, while the orbits of comets tend to be highly elongated.

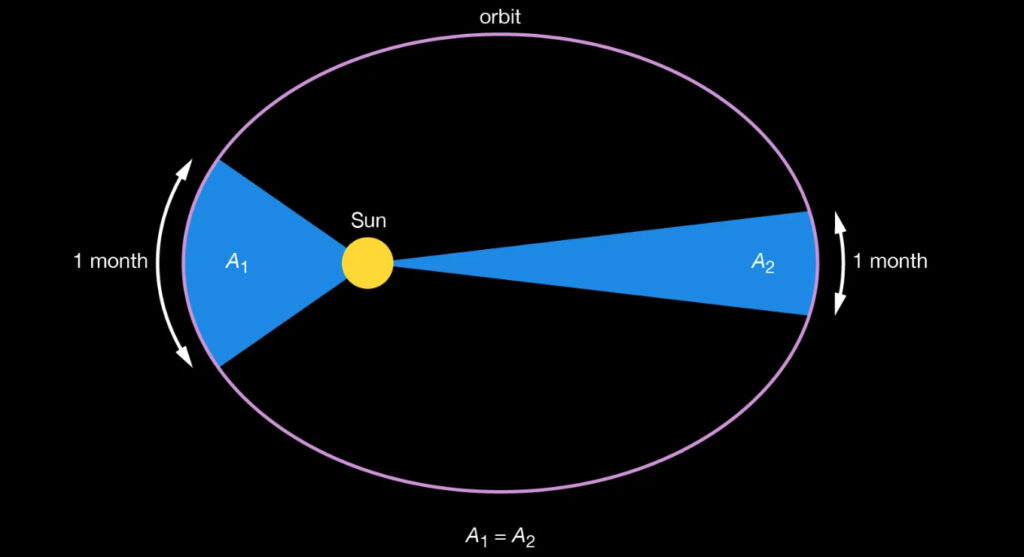
Kepler’s Second Law: The Law of Equal Areas

Kepler’s Second Law states that a line drawn from the Sun to a planet sweeps out equal areas in equal intervals of time. This means that planets move faster when they are closer to the Sun and slower when they are farther away.

To visualize this, think of a planet’s orbit divided into pie-shaped wedges. Whether the planet is near the Sun or far from it, the area of these wedges remains constant over the same period. This behaviour explains why a planet speeds up during its closest approach to the Sun (called perihelion) and slows down during its farthest point (called aphelion).

This law has practical applications in space missions. Scientists use it to calculate the speed and trajectory of spacecraft travelling to distant planets or moons. It also explains why seasons on Earth vary in length.

Kepler’s Third Law: The Harmonic Law

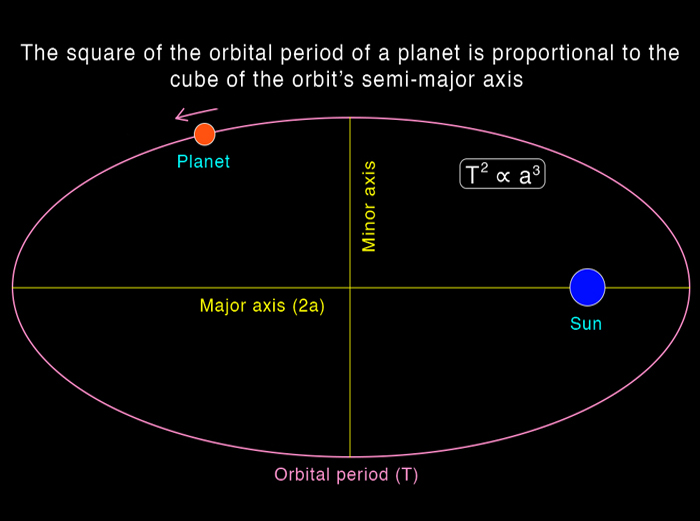
Kepler’s Third Law establishes a relationship between the time a planet takes to complete one orbit around the Sun (its orbital period) and the average distance from the Sun. Mathematically, it states that the square of a planet’s orbital period is proportional to the cube of its average distance from the Sun.

In simple terms, planets farther from the Sun take longer to orbit it. For example, Earth takes one year to complete its orbit, while Jupiter takes about 12 years. The formula for this law is:

T² ∝ R³

Here, T is the orbital period, and R is the average distance from the Sun. This law is crucial for understanding the relative distances and speeds of planets in our solar system and beyond. It also plays a key role in identifying exoplanets orbiting distant stars.

Historical Context and Kepler’s Contribution

Johannes Kepler developed these laws using meticulous observations made by Tycho Brahe. Kepler’s innovative thinking and mathematical skills allowed him to analyze Brahe’s data and uncover the true nature of planetary motion.

Before Kepler, the geocentric model of the universe—which placed Earth at the centre—dominated scientific thought. Even after the heliocentric model proposed by Copernicus gained acceptance, many believed in circular planetary orbits. Kepler’s laws provided the first accurate mathematical description of planetary motion, paving the way for Isaac Newton’s theory of gravitation.

Applications of Kepler’s Laws

Kepler’s Laws are more than just theoretical principles; they have practical implications in modern astronomy and space exploration. Here are some key applications:

1. Space Travel: Kepler’s Laws help calculate spacecraft trajectories, ensuring accurate missions to planets, moons, and asteroids. By understanding orbital dynamics, scientists can plot efficient routes, saving fuel and time.
2. Satellite Operations: Satellites orbiting Earth follow Kepler’s principles. Engineers use these laws to design stable satellite orbits for communication, weather forecasting, and navigation.
3. Exoplanet Discovery: Astronomers use Kepler’s Third Law to detect and study planets outside our solar system. By observing the motion of stars and their planets, scientists estimate their masses, distances, and orbital periods.
4. Understanding Comets: The highly elliptical orbits of comets align with Kepler’s First Law. By analyzing these orbits, astronomers can predict when comets will return to the inner solar system.

Why Are Kepler’s Laws Important?

Kepler’s Laws revolutionized our understanding of the universe. They provided evidence that celestial bodies follow predictable patterns governed by natural laws. This insight laid the groundwork for modern physics and astronomy.

Moreover, Kepler’s work demonstrated the power of observation and mathematics in uncovering the mysteries of the cosmos. His laws continue to guide scientific discoveries, from studying our solar system to exploring distant galaxies.

Conclusion

Kepler’s Laws of Planetary Motion remain a cornerstone of astronomy. They explain how planets move, why their speeds change, and how their distances relate to their orbital periods. By understanding these laws, we gain a deeper appreciation of the universe and our place within it.

Whether you are an aspiring astronomer or simply curious about the cosmos, Kepler’s Laws offer a fascinating glimpse into the harmony of the natural world. These timeless principles remind us of the enduring quest for knowledge that defines humanity.

So that’s all for today. Best wishes to all of you from Sci-fi Note. Stay well, keep the environment healthy, and maintain your love for science. Thank you.